La Ricerca Sequenziale¶
In una lista, i valori sono memorizzati uno dopo l’altro secondo il loro indice. Il processo di visita degli elementi è detto ricerca sequenziale.
Figura 1 mostra come funziona la ricerca. Partendo dall’inizio della lista, visitiamo tutti gli elementi uno dopo l’altro.
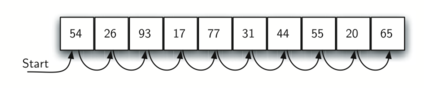
Figura 1: Ricerca Sequenziale in una Lista di Interi
La funzione mostrata in CodeLens 1, ricerca se il valore passato come argomento è presente nella lista passata come argomento.
Sequential Search of an Unordered List (search1)
Analisi della Ricerca Sequenziale¶
Per fare l’analisi, dobbiamo decidere l’unità di base della computazione. In questo caso contiamo il numero di confronti effettuati. La lista non è ordinata, quindi l’elemento da cercare potrebbe essere ovunque con la stessa probabilità.
Se l’elemento non è nella lista, allora abbiamo bisogno di \(n\) confronti. Se l’elemento è nella lista, cosa succede in media? confronteremo in media \(\frac{n}{2}\) elementi, per cui la complessità media è \(O(n)\). Tabella 1 riassume quanto detto.
| elemento presente | \(1\) | \(n\) | \(\frac{n}{2}\) |
| elemento non presente | \(1\) | \(n\) | \(n\) |
Assumiamo che la lista contenga i valori in modo ordinato. Possiamo modificare l’algoritmo visto sopra per migliorare il caso in cui l’elemento non sia presente. Figura 2 mostra cosa succede se cerchiamo 50. Se abbiamo visto che 50 non è presenta nella porzione di lista fino a 54, allora non sarà presente nella rimanente porzione della lista. In questo caso si può fermare la ricerca. CodeLens 2 mostra questa variazione.
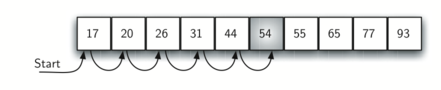
Figura 2: Ricerca Sequenziale in una Lista Ordinata di Interi
Ricerca Sequenziale in una Lista Ordinata (search2)
Tabella 2 riassume i risultati, mostrando il miglioramento nel solo caso in cui l’elemento non sia presente.
| elemento presente | \(1\) | \(n\) | \(\frac{n}{2}\) |
| elemento non presente | \(1\) | \(n\) | \(\frac{n}{2}\) |