La Ricerca Binaria¶
Invece di cercare l’elemento in sequenza, una ricerca binaria comincerà analizzando l’elemento in mezzo. Se tale elemento è quello che stiamo cercando, abbiamo finito. Altrimenti, se l’elemento che stiamo cercando è più grande dell’elemento di mezzo, ripetiamo cercandolo nella porzione destra della lista, altrimenti, se è più piccolo, cerchiamo nella porzione sinistra.
Figura 3 mostra come opera questo algoritmo mentre cerca il valore 54. La funzione completa è mostrata in CodeLens 3.
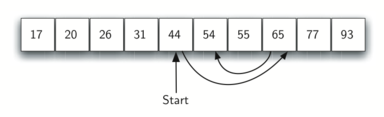
Figura 3: Ricerca Binaria in una Lista Ordinata di Interi
Ricerca Binaria in una Lista Ordinata (search3)
Questo modo di operare è un esempio del paradigma ‘divide et impera’, tecnica algoritmica per cui il problema viene diviso in problemi più piccoli e il risultato ottenuto per questi problemi viene combinato per ottenere il risultato del problema più grande. In particolare, possiamo risolvere i sottoproblemi facendo una chiamata ricorsiva, facendo una ricerca nella porzione a sinistra o nella porzione a destra. In entrambi i casi, questa è una chiamata ricorsiva passando una lista più piccola. CodeLens 4 mostra questa versione ricorsiva.
A Binary Search--Recursive Version (search4)
Analisi della Ricerca Binaria¶
Quale è il numero massimo di confronti richiesto dall’algoritmo di ricerca binaria? Se cominciamo con n elementi, rimangono circa \(\frac{n}{2}\) elementi dopo il primo confronto. Dopo il secondo confronto, ne rimangono \(\frac{n}{4}\). Successivamente \(\frac{n}{8}\), poi \(\frac{n}{16}\) e così via. Quante volte possiamo dividere la lista? Tabella 3 ci aiuta a rispondere a questa domanda.
| Confronto | Numero di elementi rimasti |
|---|---|
| 1 | \(\frac {n}{2}\) |
| 2 | \(\frac {n}{4}\) |
| 3 | \(\frac {n}{8}\) |
| … | |
| i | \(\frac {n}{2^i}\) |
Nel caso peggiore, arriviamo ad analizzare una lista grande 1. Il numero di confronti necessari per arrivare ad avere una lista grande 1, è il valore di i per cui \(\frac {n}{2^i} =1\). Risolvendo l’equazione in i, otteniamo \(i=\log n\). Per cui il numero di confronti necessari è logaritmico rispetto al numero di elementi della lista. Per cui la ricerca binaria prende tempo \(O(\log n)\).
Tuttavia, è bene notare che l’implementazione fornita sopra effettua l’invocazione
binarySearch(alist[:midpoint],item)
usando l’operazione slice per creare la partizione sinistra. Tuttavia, l’operazione di slice prende tempo O(k) e non costante (copia tutti gli elementi della porzione sinistra in un nuova lista). Questo significa, che l’implementazione sopra non prende tempo logaritmico. Possiamo rimediare passando insieme alla lista anche gli indici di inizio e fine in cui cercare. Gli indici possono essere calcolati come abbiamo fatto in Listing 3. Lasciamo questa implementazione come esercizio.
Sebbene la ricerca binaria è generalmente meglio della sequenziale essa richiede di avere la lista ordinata. Conviene ordinare la lista e pagare un costo di \(O(n\log n)\), se sappiamo che cercheremo molte volte al suo interno, altrimenti non ne vale la pena.