Ancora su programmazione dinamica: distanza tra stringhe¶
A cura di Maria Francesca Morabito
Problema e tecnica algoritmica¶
La distanza tra due stringhe è da intendersi come misura della loro dissimilarità, per calcolarla si può ricorrere alla distanza di Levenshtein. Date due stringhe X e Y di lunghezza qualsiasi, la distanza di Levenshtein rappresenta il numero minimo di modifiche da apportare alla stringa X per trasformarla in Y, in termini di:
- rimozione di un carattere
- inserimento di un carattere
- sostituzione di un carattere
Per misurare questa distanza in maniera corretta ed efficiente si ricorre alla programmazione dinamica. Questa tecnica algoritmica si basa sulla decomposizione del problema principale in sottoproblemi con intersezione non vuota e si utilizza, ad esempio, in sostituzione di algoritmi ricorsivi con complessità elevata. Infatti, grazie alla memorizzazione delle soluzioni di ogni sottoproblema, si evita che gli stessi passaggi ricorsivi vengano ripetuti più volte. Con le tecniche di programmazione dinamica vengono risolti inoltre problemi di ottimizzazione, attraverso l’unione delle soluzioni ottime dei sottoproblemi. Perché ciò avvenga è necessario che il problema abbia una sottostruttura ottimale, ovvero che l’ottimalità delle soluzioni intermedie permanga e garantisca l’ottimo generale.
Algoritmo risolutivo e codice Python¶
Nel caso del calcolo della distanza tra due stringhe, i sottoproblemi da risolvere sono relativi alla determinazione della distanza tra tutte le rispettive sottostringhe iniziali (prefissi), a partire dalle stringhe nulle fino alle stringhe complete.
Date le stringhe X di lunghezza m ed Y di lunghezza n, si definiscono:
- \(X_i\), la sottostringa costituita dai primi i caratteri di X per \(i=1,...,m\) (con \(X_0=Ø\))
- \(Y_j\), la sottostringa costituita dai primi j caratteri di Y per \(j=1,...,n\) (con \(Y_0=Ø\))
Ad ogni passo viene determinata \(\delta(X_i,Y_j)\), ovvero la distanza di Levenshtein tra \(X_i\) e \(Y_j\), per la quale vale che:
- \(\delta(X_m,Y_n)=\delta(X,Y)\), \(X_m\) coincide infatti con la stringa completa \(X\) (contenente tutti i suoi \(m\) caratteri) e \(Y_n\) coincide con la stringa completa \(Y\) (contenente tutti i suoi \(n\) caratteri);
- \(\delta(Ø,Y_j)=j\) per \(j=0,...,n\), poiché è evidente che il numero minimo di modifiche da apportare ad una stringa nulla per trasformarla nella stringa \(Y_j\) è raggiunto inserendo tutti i caratteri di \(Y_j\);
- \(\delta(X_i,Ø)=i\) per \(i=0,...,m\), in quanto, similmente al caso precedente, il numero minimo di modifiche da apportare alla stringa \(X_i\) per trasformarla in una stringa nulla è raggiunto rimuovendo i suoi \(i\) caratteri.
I sottoproblemi sono quindi \((m+1)\cdot(n+1)\), comprendendo i sottoproblemi che coinvolgono i prefissi nulli (stringhe vuote).
Secondo un approccio di tipo bottom-up, si parte da soluzioni note al livello più basso e, rispettando l’ordine tra i sottoproblemi, si risolvono gli altri. La soluzione di ogni sottoproblema si basa sulle soluzioni dei sottoproblemi precedenti, per cui esse vengono conservate e utilizzate come segue:
- se i caratteri \(x_i\) e \(y_j\) sono uguali, \(\delta(X_i,Y_j)\) è uguale a \(\delta(X_{i-1},Y_{j-1})\) in quanto non serve operare alcuna ulteriore modifica;
- se i caratteri \(x_i\) e \(y_j\) sono differenti, è necessario incrementare di una modifica il valore della metrica calcolata per i sottoproblemi immediatamente precedenti. La minimizzazione del costo di trasformazione si assicura incrementando ad ogni passo la distanza più piccola.
I passaggi dell’algoritmo sono i seguenti:
- si inizializza a zero una matrice \(D\) di dimensione \((m+1)\cdot(n+1)\), in cui verranno conservate tutte le soluzioni intermedie
- si assegnano le soluzioni ai problemi banali relativi alle distanze tra le sottostringhe di \(X\) e una stringa vuota (prefisso nullo di \(Y\)) e viceversa, ovvero: \(D[0,0]=0\), \(D[i,0]=i\) per \(i=1,...,m\) e \(D[0,j]=j\) per \(j=1,...,n\)
- tramite due cicli annidati che scorrono e confrontano tutti i caratteri delle due stringhe (per \(i=1,...,m\) e per \(j=1,...,n\)), si calcolano le soluzioni di tutti i sottoproblemi secondo i criteri discussi sopra, ovvero:
3.a. \(D[i,j]=D[i-1,j-1]\) se \(x_i=y_j\)
3.b. \(D[i,j]=1+\min (D[i-1,j-1], D[i,j-1], D[i-1,j])\) se \(x_i \neq y_j\)
In quest’ultimo caso, la soluzione utilizzata per risolvere ogni sottoproblema è legata ad una particolare modifica (sostituzione, inserimento o rimozione), secondo il seguente schema:
| Distanza incrementata | Modifica corrispondente |
|---|---|
| \(D[i-1,j-1]\) | Sostituzione |
| \(D[i,j-1]\) | Inserimento |
| \(D[i-1,j]\) | Rimozione |
Quando la soluzione da assegnare a \(D[i][j]\) è ottenuta tramite incremento unitario della distanza assegnata a \(D[i][j-1]\), si aggiunge una modifica di inserimento del carattere \(y_j\). Infatti, seguendo il percorso di modifiche la cui somma è assegnata a \(D[i][j-1]\), non si rimuove né si sostituisce il carattere \(x_i\). Un’eventuale modifica a questo carattere viene già valutata, selezionata e conteggiata per trasformare \(X_i\) in \(Y_{j-1}\). Al contrario, quando a \(D[i][j]\) si assegna la distanza \(D[i-1][j]\) incrementata di una unità, la modifica corrispondente è la rimozione di \(x_i\). In \(D[i-1][j]\) sono conteggiate le modifiche che permettono di trasformare i primi \(i-1\) caratteri di \(X\) nella sottostringa di \(Y\) che contiene già il carattere \(y_j\), per cui non avrebbe senso inserirlo né porlo in sostituzione di \(x_i\). Infine, incrementando \(D[i-1][j-1]\), le modifiche a cui se ne aggiunge una nuova non coinvolgono né il carattere \(x_i\) né il carattere \(y_j\) ed è conveniente sostituire direttamente il primo con il secondo.
La traduzione dell’algoritmo in codice Python consiste in una funzione che riceve in input le due stringhe di cui calcolare la distanza di Levenshtein. Una volta richiamata la funzione, essa restituisce il costo minimo di trasformazione di una nell’altra, ovvero l’ultimo valore inserito nella matrice (corrispondente a \(\delta(X_m,Y_n)\)).
def Distance(str1,str2):
# Inizializzazione a zero della matrice di dimensione (m+1)x(n+1)
m=len(str1)+1
n=len(str2)+1
D = [[0 for k in range(n)] for k in range(m)]
# Assegnazione delle soluzioni ai problemi banali
for i in range(1,m):
D[i][0]=i
for j in range(1,n):
D[0][j]=j
# Cicli annidati per la risoluzione dei sottoproblemi
for i in range(1,m):
for j in range(1,n):
# Se i caratteri sono diversi
if str1[i-1]!=str2[j-1]:
D[i][j]=1+min(D[i][j-1],D[i-1][j],D[i-1][j-1])
# Se i caratteri sono uguali
else:
D[i][j]= D[i-1][j-1]
# Restituisce la soluzione del problema
return D[len(str1)][len(str2)]
Esempio¶
Per conoscere “quanto non sono simili” le parole look e alike, si stampa il risultato della chiamata della funzione Distance.
print(Distance("look","alike"))
Il risultato dell’algoritmo indica che la trasformazione di look (X) in alike (Y) consiste al minimo in 4 modifiche che possono essere:
- Aggiunta di \(y_1\) (A)
- Sostituzione di \(x_2\) con \(y_3\) (O con I)
- Rimozione di \(x_3\) (O)
- Aggiunta di \(y_5\) (E)
| - | L | O | O | K | - |
| A | L | I | - | K | E |
La matrice calcolata dalla funzione Distance è mostrata in figura (qualora sia richiesto, si può aggiungere agli output), dove è indicato in rosso un possibile percorso di modifiche.
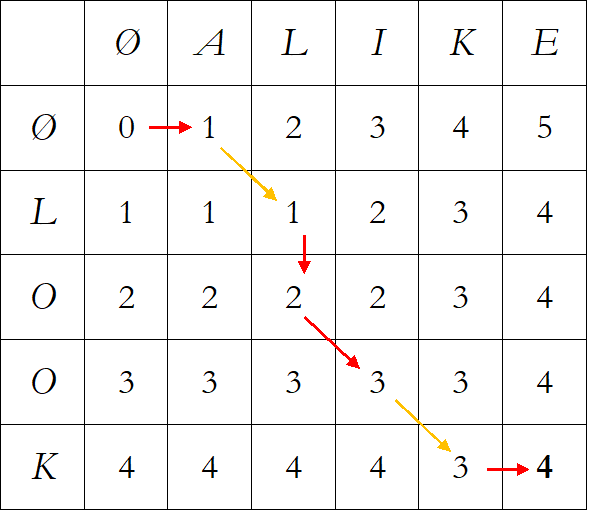
Per le stringhe dell’esempio, il passaggio 3.b dell’algoritmo viene compiuto confrontando valori delle tre celle per le quali la determinazione del minimo non è sempre univoca (e di conseguenza non è sempre univoca la scelta tra sostituzione, eliminazione e aggiunta del carattere), sono possibili quindi diversi schemi di modifiche applicabili alla stringa look per trasformarla in 4 passaggi nella stringa alike.
Complessità computazionale¶
La complessità computazione di un algoritmo viene calcolata valutando le risorse necessarie per la sua esecuzione, le quali possono essere riferite al tempo e/o allo spazio. Indipendentemente dalla macchina e dal linguaggio adoperati, il tempo può essere calcolato come numero di istruzioni contenute nell’algoritmo.
Il tempo¶
Il tempo computazionale dell’algoritmo in analisi ha un ordine di grandezza pari a \(O(mn)\). Tale complessità dipende esclusivamente dalla lunghezza delle stringhe, a prescindere dai caratteri contenuti in esse. Per questo motivo si tratta di un costo polinomiale puro.
Più nel dettaglio, l’algoritmo consiste in:
- operazioni di assegnamento preliminari
- \(m+n\) assegnamenti in due cicli separati, per il riempimento della prima riga e della prima colonna della matrice D (ad eccezione della cella \(D[0,0]\))
- \(mn\) istruzioni, in due ulteriori cicli annidati tra loro, per completare il riempimento della matrice
La parte dominante del tempo di esecuzione, ovvero quella che assume maggiore rilevanza al crescere delle lunghezze delle stringhe, è appunto \(f(m,n)=mn\).
Algoritmo ricorsivo vs Algoritmo a programmazione dinamica¶
Il problema della distanza tra stringhe può essere risolto correttamente anche tramite ricorsione. Come per ogni procedura ricorsiva, è necessario individuare un caso base. Per il problema in analisi, esso si verifica quando almeno una delle due stringhe ha lunghezza nulla.
La funzione Distance2 restituisce la distanza di Levenshtein corretta, richiamando se stessa tre volte ogni volta che viene (ri)chiamata. Si tratta quindi di ricorsioni multiple che rendono l’algoritmo meno efficiente del precedente.
def Distance2(str1, str2):
if len(str1) == 0:
return len(str2)
if len(str2) == 0:
return len(str1)
if str1[-1] != str2[-1]:
return min(1 + Distance2(str1[:-1], str2), 1 + Distance2(str1, str2[:-1]),
1 + Distance2(str1[:-1], str2[:-1]))
else:
return Distance2(str1[:-1], str2[:-1])
È possibile comparare il tempo impiegato per risolvere lo stesso problema con le due funzioni utilizzando il modulo time di Python. I risultati riportati in tabella sono i tempi medi di esecuzione (in secondi) relativi a 10 chiamate delle funzioni Distance e Distance2, passando le due stesse coppie di argomenti.
| Strings | ||
| Functions | Look - Alike | Information - Informatics |
Distance |
0.0 | 0.0001988 |
Distance2 |
0.0005 | 32.677819 |
Si può notare la dipendenza del tempo impiegato dalla lunghezza delle stringhe e la maggiore efficienza dell’algoritmo a programmazione dinamica. Ciò è dovuto al fatto che nel caso ricorsivo le soluzioni intermedie non vengono memorizzate ma ri-calcolate tutte le volte che servono tramite una chiamata multipla della funzione a se stessa. Per questo motivo, il tempo computazione impiegato dall’algoritmo ricorsivo cresce esponenzialmente al crescere delle lunghezze delle stringhe. Nel peggiore dei casi, ovvero se le due stringhe non hanno nessun carattere in comune, il percorso più lungo di chiamate ricorsive è quello che si ottiene togliendo alternativamente un carattere di \(X\) e uno di \(Y\), raggiungendo una complessità pari a \(O(3^{m+n-1})\).
Lo spazio¶
Come appena sottolineato, il vantaggio computazione dell’algoritmo a programmazione dinamica è apportato dalla memorizzazione delle soluzioni intermedie. Questa tecnica è detta memoizzazione, che significa letteralmente “mettere in memoria”. Tuttavia, per riempire una nuova cella della matrice è necessario conoscere esclusivamente il valore di tre celle (e conservare le righe di cui fanno parte). In particolare, per il calcolo di ogni \(\delta(X_i,Y_j)\), serve conoscere \(\delta(X_{i-1},Y_{j-1} )\), \(\delta(X_{i},Y_{j-1} )\) e \(\delta(X_{i-1},Y_{j} )\).
È quindi sufficiente uno spazio minore di quello allocato con la funzione Distance. Richiamando la funzione Distance3, infatti, le risorse computazionali utilizzate in termini di spazio vengono ridotte a due vettori della lunghezza della seconda stringa, passando da un ordine di grandezza \(O(nm)\) a \(O(n)\). Il risultato restituito in output è ugualmente corretto.
def Distance3(str1,str2):
m = len(str1) + 1
n = len(str2) + 1
F = [k for k in range(n)]
for i in range(1,m):
S = [0 for k in range(n)]
S[0] = i
for j in range(1,n):
if str1[i-1]!=str2[j-1]:
S[j]=1+min(S[j-1],F[j-1],F[j])
else:
S[j]= F[j-1]
F = S
return F[-1]