The Bubble Sort¶
The bubble sort makes multiple passes through a list. It compares adjacent items and exchanges those that are out of order. Each pass through the list places the next largest value in its proper place. In essence, each item “bubbles” up to the location where it belongs.
Figure 1 shows the first pass of a bubble sort. The shaded items are being compared to see if they are out of order. If there are n items in the list, then there are \(n-1\) pairs of items that need to be compared on the first pass. It is important to note that once the largest value in the list is part of a pair, it will continually be moved along until the pass is complete.
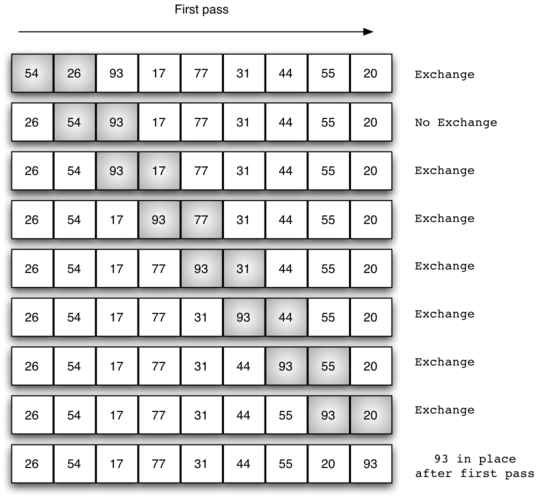
Figure 1: bubbleSort: The First Pass
At the start of the second pass, the largest value is now in place.
There are \(n-1\) items left to sort, meaning that there will be
\(n-2\) pairs. Since each pass places the next largest value in
place, the total number of passes necessary will be \(n-1\). After
completing the \(n-1\) passes, the smallest item must be in the
correct position with no further processing required. ActiveCode 1
shows the complete bubbleSort function. It takes the list as a
parameter, and modifies it by exchanging items as necessary.
The exchange operation, sometimes called a “swap,” is slightly different in Python than in most other programming languages. Typically, swapping two elements in a list requires a temporary storage location (an additional memory location). A code fragment such as
temp = alist[i]
alist[i] = alist[j]
alist[j] = temp
will exchange the ith and jth items in the list. Without the temporary storage, one of the values would be overwritten.
In Python, it is possible to perform simultaneous assignment. The
statement a,b=b,a will result in two assignment statements being
done at the same time (see Figure 2). Using simultaneous
assignment, the exchange operation can be done in one statement.
Lines 5-7 in ActiveCode 1 perform the exchange of the \(i\) and \((i+1)th\) items using the three–step procedure described earlier. Note that we could also have used the simultaneous assignment to swap the items.
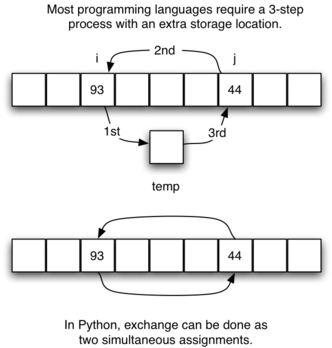
Figure 2: Exchanging Two Values in Python
The following activecode example shows the complete bubbleSort function working on the list
shown above.
The Bubble Sort (lst_bubble)
The following animation shows bubbleSort in action.
To analyze the bubble sort, we should note that regardless of how the items are arranged in the initial list, \(n-1\) passes will be made to sort a list of size n. Table 1 shows the number of comparisons for each pass. The total number of comparisons is the sum of the first \(n-1\) integers. Recall that the sum of the first n integers is \(\frac{1}{2}n^{2} + \frac{1}{2}n\). The sum of the first \(n-1\) integers is \(\frac{1}{2}n^{2} + \frac{1}{2}n - n\), which is \(\frac{1}{2}n^{2} - \frac{1}{2}n\). This is still \(O(n^{2})\) comparisons. In the best case, if the list is already ordered, no exchanges will be made. However, in the worst case, every comparison will cause an exchange. On average, we exchange half of the time.
| Pass | Comparisons |
|---|---|
| 1 | \(n-1\) |
| 2 | \(n-2\) |
| 3 | \(n-3\) |
| … | … |
| \(n-1\) | \(1\) |
A bubble sort is often considered the most inefficient sorting method since it must exchange items before the final location is known. These “wasted” exchange operations are very costly. However, because the bubble sort makes passes through the entire unsorted portion of the list, it has the capability to do something most sorting algorithms cannot. In particular, if during a pass there are no exchanges, then we know that the list must be sorted. A bubble sort can be modified to stop early if it finds that the list has become sorted. This means that for lists that require just a few passes, a bubble sort may have an advantage in that it will recognize the sorted list and stop. ActiveCode 2 shows this modification, which is often referred to as the short bubble.
The Short Bubble Sort (lst_shortbubble)
Self Check