Liste¶
Due operazioni comuni sono indicizzazione e assegnamento a una specifica posizione. Entrambe prendono lo stesso tempo indipendentemente dalla grandezza della lista. Per cui si dice che il tempo richiesto è \(O(1)\).
Un’altra operazione molto richiesta è quella di far crescere una lista. Ci sono due modi per farlo, usando il metodo append o la concatenazione. Il metodo append richiede \(O(1)\) (quasi sempre), mentre la concatenazione richiede \(O(k)\) dove \(k\) è la grandezza della dimensione della lista da concatenare.
Di seguito analizziamo quattro modi per creare una lista di n numeri partendo da dimensione 0.
- Prima, usiamo un
fore creiamo la lista usando la concatenazione, - Poi usiamo append invece della concatenazione.
- Poi usiamo la comprensione di lista,
- Poi usiamo la funzione range (convertita in lista).
Listing 3 mostra il codice per creare le liste nei quattro modi esposti.
Listing 3
def test1():
l = []
for i in range(1000):
l = l + [i]
def test2():
l = []
for i in range(1000):
l.append(i)
def test3():
l = [i for i in range(1000)]
def test4():
l = list(range(1000))
Per catturare il tempo possiamo usare il modulo timeit, che è pensato per fare confronti di tempo eseguendo Python in un ambiente controllato con performance quanto più indipendenti dal sistema operativo.
Per usare timeit creiamo un oggetto Timer i cui parametri sono due istruzioni.
- Il primo parametro è una istruzione Python che vogliamo misurare.
- Il secondo parametro è una istruzione che verrà eseguita una volta prima dell’esecuzione del test per fare il setup.
Di default timeit esegue l’istruzione 1 milione di volte e ritorna il tempo totale. In alternativa è possibile passare il numero di esecuzioni, come sotto, specificando il valore del parametro opzionale number.
t1 = Timer("test1()", "from __main__ import test1")
print("concat ",t1.timeit(number=1000), "milliseconds")
t2 = Timer("test2()", "from __main__ import test2")
print("append ",t2.timeit(number=1000), "milliseconds")
t3 = Timer("test3()", "from __main__ import test3")
print("comprehension ",t3.timeit(number=1000), "milliseconds")
t4 = Timer("test4()", "from __main__ import test4")
print("list range ",t4.timeit(number=1000), "milliseconds")
concat 6.54352807999 milliseconds
append 0.306292057037 milliseconds
comprehension 0.147661924362 milliseconds
list range 0.0655000209808 milliseconds
In questo caso from __main__ import test1 importa la funzione test1 dal __main__ dentro timeit per effettuare l’esperimento. Il modulo timeit fa questa cosa per disaccoppiarsi da qualsiasi altra variabile potremmo aver creato che potrebbe interferire con i tempi.
Tabella 2 mostra il costo delle operazioni sulle liste.
Notiamo che quando pop è chiamato in fondo alla lista richiede
\(O(1)\), ma quando viene chiamata su qualsiasi altro indice richiede \(O(n)\), perché tutti gli elementi successivi vengono spostati di una posizione in avanti.
| Operazione | Efficienza |
|---|---|
| index [] | O(1) |
| index assignment | O(1) |
| append | O(1) |
| pop() | O(1) |
| pop(i) | O(n) |
| insert(i,item) | O(n) |
| del operator | O(n) |
| iteration | O(n) |
| contains (in) | O(n) |
| get slice [x:y] | O(k) |
| del slice | O(n) |
| set slice | O(n+k) |
| reverse | O(n) |
| concatenate | O(k) |
| sort | O(n log n) |
| multiply | O(nk) |
Il codice seguente mostra le diverse performance nell’usare pop. L’istruzione from __main__ import x richiede di importare l’oggetto x dal main.
Listing 4
popzero = timeit.Timer("x.pop(0)",
"from __main__ import x")
popend = timeit.Timer("x.pop()",
"from __main__ import x")
x = list(range(2000000))
popzero.timeit(number=1000)
4.8213560581207275
x = list(range(2000000))
popend.timeit(number=1000)
0.0003161430358886719
Il testo sopra ha mostrato che pop(0) è più lento di
pop(). Vogliamo adesso mostrare che pop(0) prende
\(O(n)\) tempo mentre pop() prende \(O(1)\).
Listing 5
popzero = Timer("x.pop(0)",
"from __main__ import x")
popend = Timer("x.pop()",
"from __main__ import x")
print("pop(0) pop()")
for i in range(1000000,100000001,1000000):
x = list(range(i))
pt = popend.timeit(number=1000)
x = list(range(i))
pz = popzero.timeit(number=1000)
print("%15.5f, %15.5f" %(pz,pt))
Figura 3 mostra i risultati del nostro esperimento, mostrando che al crescere della dimensione della lista, pop(0) richiede più tempo mentre il tempo di pop rimane lo stesso.
Errori di misurazione e fluttuazioni dipendono dal fatto che potremmo stare eseguendo diversi altri processi sul nostro computer. Per questo il test viene ripetuto più volte.
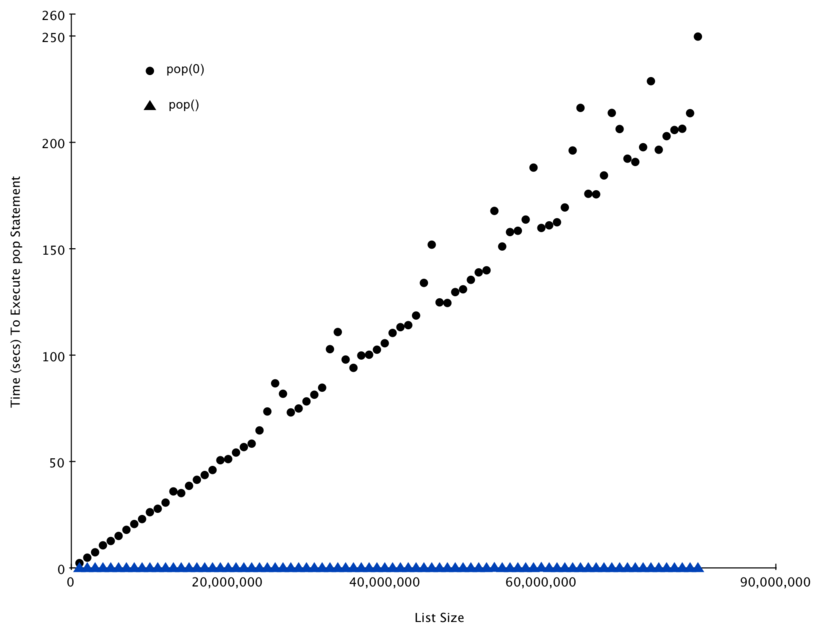
Figura 3: Confronto dei tempi richiesti da pop e pop(0)
Il costo dell’append abbiamo detto che è \(O(1)\) quasi sempre. Cosa intendiamo? Questo costo si riferisce in realtà al costo di complessità ammortizzata, ovvero il costo medio di m aggiornamenti fatti in sequenza, considerando la sequenza peggiore. Questo è diverso dalla complessità del caso medio, perché nella complessità ammortizzata gli inserimenti che facciamo pescando dalla sequenza di m operazioni sono dipendenti l’uno dall’altro e stiamo considerando la sequenza peggiore. Riguardo alla complessità ammortizzata quindi, azioni individuali potrebbero richiedere tempo sorprendentemente lungo, dipendentemente dalla storia della lista.